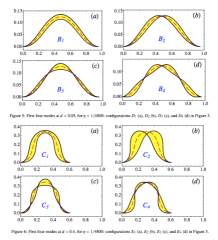
The small-amplitude in-plane vibrations of an elastic rod clamped at both extremities are studied. The rod is modeled as an extensible, shearable, planar Kirchhoff elastic rod under large displacements and rotations, and the vibration frequencies are computed both analytically and numerically as a function of the loading. Of particular interest is the variation of mode frequencies as the load is increased through the buckling threshold. While for some modes there are no qualitative changes in the mode frequencies, other frequencies experience rapid variations after the buckling threshold, the thinner the rod, the more abrupt the variations. Eventually, a mismatch for half of the frequencies at buckling arises between the zero thickness limit of the extensible model and the inextensible model.